This is simple Matrix library to perform Matrix operations namely Matrix Multiplication and Transpose. The library is divided into 2 parts, one for Matrix operations on small Matrices (class Matrix) and other for Large Matrices (class BigMatrix). The complete code documentation generated by Doxygen can be found here. Video explanation of the library can be found here.

Matrix multiplication for small matrices is done using the straight forward solution with time complexity O(n^3). While for large matrices the Matrix multiplication is done using the Strassen's Algorithm that has Time Complexity of approximately O(n^2.8).

For Large Matrices the input is taken in a Comma Separated Variable (csv) file format, and the output is stored in a csv file. For small matrices the user has to manually enter the values of the matrix either using a initializer_list format or as a 2D vector.

Installation and Configuration

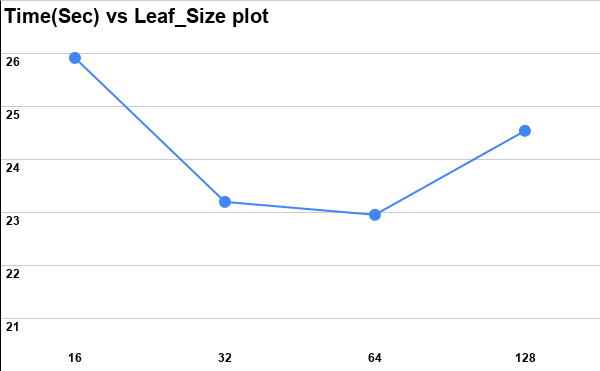
Inorder to get the best performance from this library for large Matrix Multiplicaiton, one has to experimentally find out and set the LEAF_SIZE for the Strassen's Multiplcation function. The LEAF_SIZE value modifies the Resursion base condition. Once a Matrix of size LEAF_SIZE x LEAF_SIZE or lesser is reached we shift to the Native O(n^3) Matrix Multiplication solution. The Value of LEAF_SIZE has the following effect on the library:

A very high value of LEAF_SIZE leads to lesser resursion calls but ends up giving more weightage to the O(n^3) solution, thus suffer high execution time.
On the other hand a very low LEAF_SIZE value leads to higher number of resursion calls and gives lesser weightage to the O(n^3) solution, which again leads to high execution time.

Both the above scenarios adversely effects the execution time of Matrix Multiplication and added to that the value of optimal LEAF_SIZE will vary from machine to machine. Thus we have to experimentally determine the LEAF_SIZE value from the computer on which this library will be used. In order to do this a configure_lib.cpp file and is provided with this library. This file performs Matrix Multiplication between 2 large matrices A & B (stored as A.csv and B.csv in Configure_Data folder) using the matmul function (defined in class BigMatrix). Configure_lib.cpp performs the multiplication for N_epoch no. of times (N_epoch >2) for a given LEAF_SIZE and finds the average execution times for this particular LEAF_SIZE. It continues doing the same for LEAF_SIZE=16, 32,64 ..... as the average execution times keeps reducing. As soon as the value of average execution times starts increasing we break out of the inifinite while loop and store the LEAF_SIZE value that gave the least average execution times in a configure.txt file. This file is later used by matmul to multiply big matrices. The command to find the optimal LEAF_SIZE and generate the configure.txt is as follows :

$ git clone https://github.com/notu97/Matrix-Library.git matrix_WS
$ cd matrix_WS/
$ g++ configure_lib.cpp -o configure_lib -DSET_LEAF_SIZE
$ ./configure_lib <N_epoch>

Once configuration is complete, just put the matrix.h header file in the C++ working directory and include it in the main cpp code using #include"matirx.h". Also please make sure to keep the configure.txt generated during the configuration step, in the same directory as "matrix.h" i.e. the C++ working directory. An example.cpp template file is provided to get started.

On my computer, for two Matrices A.csv and B.csv of size 2000x2000 of integer type and N_epoch= 10 the optimal LEAF_SIZE was found out to be 64 i.e. once we encounter an array of size less than or equal to 64x64 we shift to O(n^3) solution for Matrix Multiplication. A plot of execution time as a function of LEAF_SIZE for my computer is shown below.

Usage

Matrix Class (for small Matrices)

Defining a small Matrix of size 3x4 of type float

Using initilizer list

MATOPS::Matrix<float,3,4> A{{1,2,3,4},{5,6,7,8},{9,10,11,12}};

Using 2D std::vector

std::vector<std::vector<float>> vect {{1,2,3,4},{5,6,7,8},{9,10,11,12}};

MATOPS::Matrix<float,3,4> A(vect);

Waring: The size of small Matrices should not exceed 200 i.e. at max we have a matrix of size 200 x 200, else the program stack gets filled with data and there is no space left to do other operations.\

#### Transposing a small Matrix

MATOPS::Matrix<float,3,4> A{{1,2,3,4},{5,6,7,8},{9,10,11,12}};

std::cout<< A.transpose();

#### Multiplying 2 small Matrices

MATOPS::Matrix<float,3,4> A{{1,2,3,4},{5,6,7,8},{9,10,11,12}};
MATOPS::Matrix<float,4,2> B{{1,2},{5,6},{9,10},{3,4}};
MATOPS::Matrix<float,3,2> C=A*B;
std::cout<< C;
//OR
std::cout<<A*B;

BigMatrix Class (for large Matrices)

Since big Matrices are already defined in a csv file, we can just parse the files and find out the dimensions of the matrix. The only information to be given to the header file is the Datatype of the Matrix.

BigMatrix Multiply (Strassen's Algorithm)

Let there be 2 matrices A and B stored in 2 csv files namely A.csv and B.csv repectively. We wish to multiply both of them and store the result in a third file named Ans.csv . The code for this process is shown below.

MATOPS::BigMatrix<float> MatObj; // Defining a Matrix object
// Multiplying the two Matrices A.csv, B.csv and storing the result in Ans.csv
MatObj.matmul("/path/to/A.csv","/path/to/B.csv","/path/to/Ans.csv");
MatObj.Mat_print("/path/to/Ans.csv"); // Printing the Answer

BigMatrix Transpose

Given a matrix A in A.csv file, we wish to find out its transpose and store it in a new file A_trans.csv

MATOPS::BigMatrix<float> MatObj; // Defining a Matrix object
MatObj.Transpose("/path/to/A.csv", "/path/to/A_trans.csv"); // Transposing the matrix and store in a A_trans.csv
MatObj.Transpose("/path/to/A.csv"); // In-place Matrix transpose.
MatObj.Mat_print("/path/to/A_trans.csv"); // Printing the result

Example code

This is an example code to illustrate how to use the library.

#include<iostream>
#include "matrix.h"
#include<vector>
using namespace std;
using namespace MATOPS; //namespace for matrix.h
int main() {
        // Define matrices of size 2x4 and 2x2 of type double using Initializer List
        Matrix<double,2,4> B{{1,2,4,5},{4,6,7,8}}; 
        Matrix<double,2,2> A{{1,2},{2,2}};
        // Print the Matrices A and B followed by Product A*B and transpose of A
        cout<<A<<"\n \n"<<B<<"\n \n"<< A*B<<"\n\n"<<A.transpose()<<"\n\n";
        BigMatrix<float> MatObj; // Define float object for Big Matrix
        // Multiply two Matrices in .csv format and save the result in Ans.csv file.
        MatObj.matmul("/path/to/A.csv","/path/to/B.csv","/path/to/Ans.csv");
        // Read Matrix A from A.csv, find its Transpose and save it in A_trans.csv
        MatObj.Transpose("/path/to/A.csv", "/path/to/A_trans.csv");
        // In-place Transpose: Read Matrix A from A.csv, find its Transpose and overwrite A.csv
        MatObj.Transpose("/path/to/A.csv");
        // print Matrix in file A.csv
        MatObj.Mat_print("/path/to/A.csv");
        return 0;
}

Terminal command to run example.cpp file is as follows:

$ g++ example.cpp -o example && ./example

Future Extension

I have kept the matrix.cpp file empty for adding future functionalities/extensions to the existing library.